अनुक्रमणिका
लेखनसार
प्रास्ताविक
शब्दखेळाची चौकट
प्रयोगनिष्पत्ती आणि विश्लेषण
भाष्य
मूळ आधारसामग्री आणि प्रयोगाचे दुवे
- - - -
प्रयोगनिष्पत्ती आणि विश्लेषण
वाक्यांचा वंशवृक्ष
वाक्यांचा वंशवृक्ष पुढील आकृतीमध्ये चितारलेला आहे. दहा पिढ्या एकाखाली एक मांडलेल्या आहेत. वाक्य रंगीत चौकोनांमध्ये लिहिलेली आहेत. चौकोनांचे रंग वाक्याला कौलामध्ये मिळालेली मतांची टक्केवारी दर्शवतात. प्रत्येक पिढीतल्या कौलामध्ये बाद झालेल्या वाक्यांवर "वर्तुळावर तिरकी रेघ" असा शिक्का मारलेला आहे. वाक्यांमधील जनक-संतान नाती बाणांनी दर्शनलेली आहेत. "जुळ्या" वाक्यांभोवती तुटक रेषेचा चौकोन काढलेला आहे.
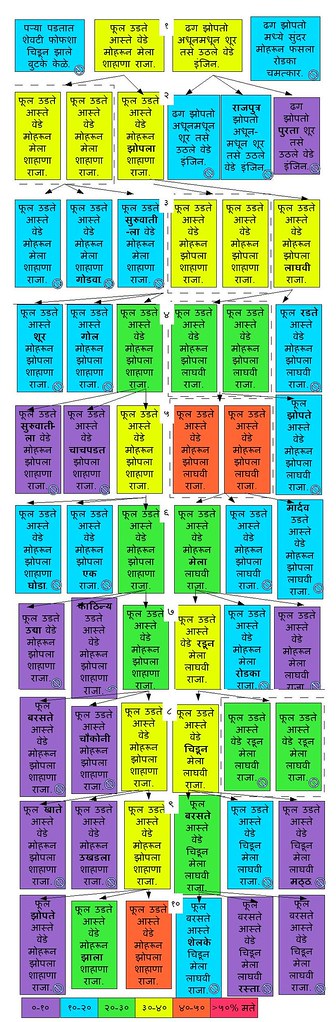
निरीक्षण १:
पहिल्या पिढीनंतर कौलातली पर्यायी वाक्ये एखाद्या-एखाद्या शब्दाच्याच फरकाची दिसतात. यामुळे कौलात निवड करणे कठिण जात होते, असे एका खेळाडूने सांगितले. असे असूनही बहुतेक पिढ्यांमध्ये निवड झालेली वाक्ये मोठ्या बहुमताने निवडून आली. यावरून असे दिसते की अर्थवत्ता आणि आस्वादसौंदर्याच्या बाबतीत सकृद्दर्शनी संदिग्धता वाटली, तरी काहीतरी सूक्ष्म आवडनिवडीबाबत खेळाडूंचे मत जुळत असावे.
निरीक्षण २:
संततीपैकी एक तरी वाक्य "काहीच बदल नाही" असे असते. अशी अभेद-रूपात वाक्ये किती पिढ्या तगली?
२६ वाक्ये केवळ एक पिढी तगली
५ वाक्ये दोन पिढ्यांपर्यंत तगली
१ वाक्य तीन पिढ्या तगले : फूल उडते आस्ते वेडे मोहरून मेला शहाणा राजा.
१ वाक्य ४ पिढ्या तगले : फूल उडते आस्ते वेडे मोहरून झोपला लाघवी राजा.
१ वाक्य ९ पिढ्या तगले : फूल उडते आस्ते वेडे मोहरून झोपला शहाणा राजा.
निरीक्षण ३:
त्यातही "लाघवी" हा शब्द वेगवेगळ्या अन्य बदलांबरोबर ७ पिढ्या तगला. त्यातील पुढील उपजाती एक-एकदा तरी कौलात जिंकली.
- फूल उडते आस्ते वेडे मोहरून झोपला लाघवी राजा.
- फूल उडते आस्ते वेडे मोहरून मेला लाघवी राजा.
- फूल उडते आस्ते वेडे चिडून मेला लाघवी राजा.
निरीक्षण ४:
सातव्या-आठव्या पिढीत "लाघवी" वाक्याला "शहाणा" वाक्यापेक्षा अधिक किंवा समान मते मिळाली. मात्र नावव्या पिढीत "लाघवी" शब्द असलेली वाक्ये नि:शेष झाली. त्यावरून असे दिसते, की मागल्या पिढ्यांमधील साफल्यामुळे पुढल्या पिढीतल्या साफल्याची काहीच शाश्वती नाही.
(क्रमशः)


प्रतिक्रिया
23 Apr 2010 - 8:33 am | राजेश घासकडवी
विश्लेषण खूप अभ्यासपूर्वक आणि कष्ट घेऊन केलेलं आहे. विशेषत: रंगतक्त्यामुळे व त्यातील वंशावळीच्या रेषा, जुळ्यांची मांडणी यामुळे प्रयोगातली सर्व माहिती एकत्रितपणे संकलित झाली आहे.
काही आणखी निरीक्षणं..
१. प्रयोग चालू असताना जुळ्यांचं प्रमाण खूप अधिक आहे असं वाटत होतं. पण इथे बघता, एकंदरीत ५४ जन्मांपैकी ५ जुळी आहेत. सुमारे १०:१ प्रमाणात. हे अपेक्षित आहे.
२. पिढी क्र. ३ मध्ये एक फांदी कापली गेली. पण त्यानंतर त्या दोन फांद्या स्वतंत्रपणे जगल्या.
हे तितकं उघड नाही वाटलं. यदृच्छेने मतदान झालं तर लाल, पिवळ्या, हिरव्याचं डिस्ट्रीब्यूशन काय राहिलं असतं?
जांभळे - १४
निळे - १८
हिरवे - १०
पिवळे - १३
लाल - ३
वरवर बघता जांभळे व निळे संख्येने अपेक्षेपेक्षा अधिक आहेत - तेव्हा या म्हणण्यात थोडं तथ्य आहे. अर्थात एक वाक्य ९ पिढ्या टिकलं हा जास्त सबळ पुरावा आहे.
छान.
24 Apr 2010 - 4:23 am | धनंजय
हे गणित वाटते तितके सोपे नाही. एका कागदाच्या तुकड्यावर मला तरी जमले नाही.
कागदावर गणित (अनॅलिटिकल सोल्यूशन) शक्य आहे, हे माहीत असूनही मी आळस केला. हे गणित मी माँतेकार्लो सिम्युलेशनांनी केले. दहा खेळाडू असलेले १५ पर्यायांचा कौल (अगदी प्रयोगातल्यासारखे) बनवला. प्रत्येक कौलात रँडम यदृच्छेने मते दिली. मते प्रयोगातल्यासारखी मोजली. असे १०,००० कौल खेळले.
कौलस्थिती १ : जर जुळी नसती तर ६ समसमान पर्याय असते. तर रंगांचे यादृच्छिक डिस्ट्रिब्यूशन असे मिळाले. (लक्षात असू द्या, की पर्यायांच्या अनुसार कमीतकमी दोन वाक्यांना मते मिळणारच होती. त्यामुळे सर्वाधिक मते फक्त ५०% मिळू शकतात.)
जांभळे - १०%
निळे - ४५%
हिरवे - ३६%
पिवळे - ७%
लाल - ०%
(५४ चौकोनांपैकी किती कुठल्या रंगांचे ते गणित ढोबळपणे : जांभळे ६, निळे २४, हिरवे २०, पिवळे ४, लाल ०)
कौलस्थिती २: जर ६ पैकी २ वाक्ये परस्पर-जुळी असतील तर रंगांचे काय डिस्ट्रिब्यूशन येईल? (जुळ्यांच्या मतांची बेरीज होते, त्या वाक्याला ५०% पेक्षा अधिक मते मिळणे शक्य होते.)
जांभळे - २४%
निळे - ५५%
हिरवे - १७%
पिवळे - ३%
लाल - ०%
(येथे जुळ्यांना "एक-चौकोन" म्हणून मोजायचे आहे, मग वरील डिस्ट्रिब्यूशन मिळते. ५०% पेक्षा अधिक मते शक्य असली तरी >५०% स्कोअरचे अपेक्षित डिस्ट्रिब्यूशन ~०.२% आहे!)
कौलस्थिती २अ : चित्रामध्ये मात्र जुळ्यांचे दोन चौकोन काढलेले आहेत, तुटक चौकोनाने जोडले असले तरी दृष्टीस दोन चौकोन म्हणून दिसतात. जुळ्याचे दोन चौकोन मोजल्यास रंगांचे डिस्ट्रिब्यूशन असे :
जांभळे - २०%
निळे - ५०%
हिरवे - २४%
पिवळे - ५%
लाल - ०%
खालच्या ९ पिढ्याच (५४ चौकोन) घेतल्या (पहिल्या पिढीत केवळ चार वाक्ये आहेत, त्याचे सिम्युलेशन मी केलेले नाही) तर :
लाल चौकोन २ (जुळ्यांसह) किंवा ३ दिसतात. अपेक्षित होते ० - वरील कुठल्याही डिस्ट्रिब्यूशनमध्ये.
पिवळे चौकोन ९ (जुळ्यांसह) किंवा ११ दिसतात. अपेक्षित होते ३-७%, म्हणजे २ किंवा ३ - वरील कुठल्याही डिस्ट्रिब्यूशनमध्ये.
लाल, पिवळे, जांभळे चौकोन दिसण्याचे प्रमाण यदृच्छेपेक्षा खूप अधिक आहे. आणि १० ऐवजी २० यादृच्छिक खेळाडू घेतले असते, तर रंग मध्यवर्ती अपेक्षेच्या आणखी जवळ गेले असते - म्हणजे निळे-हिरवेच अधिक दिसले असते. २० यादृच्छिक खेळाडूंमध्ये लाल-पिवळे नास्तिप्राय झाले असते. वास्तविक प्रयोगात १०-२० खेळाडूंनी भाग घेतला.
(सहज [बॅक-ऑफ-द-एन्व्हलप] केलेल्या अॅनॅलिटिकल गणितातून वेगळे डिस्ट्रिब्यूशन येत असल्यास त्या गणिताची गृहीतक चौकट काळजीपूर्वक जोखावी. सिम्युलेशनची चौकट साक्षात कौलच आहे.)
स्पर्धेतील बहुमताबद्दलचे निरीक्षण "क्रॉस-सेक्शनल" आहे. एक वाक्य नऊ पिढ्या टिकले, हे निरीक्षण "लाँजिट्यूडिनल" आहे. दोन्ही निरीक्षणे बरोबर असली तरी तर्कदृष्टीने समसमान नव्हेत.
24 Apr 2010 - 5:06 am | राजेश घासकडवी
सिम्युलेशनवरून प्रत्यक्षात लाल व पिवळे जास्त आहेत हे उघड आहे (मला जांभळे निळे जास्त वाटत होते...).
मला वाटतं "लाँजिट्यूडिनल" निरीक्षण, जेव्हा असेल तेव्हा ते जास्त प्रबळ असावं. म्हणजे "क्रॉस सेक्शनल" निरीक्षण आहे, पण "लाँजिट्यूडिनल" नाही हे शक्य आहे, पण "लाँजिट्यूडिनल" असताना "क्रॉस सेक्शनल" देखील दिसावं. म्हणजे एखादा लोकल मिनिमा इतका प्रबळ आहे, की त्याची इतर अनेक बदलांशी तुलना करून तो जिंकतो. "लाँजिट्यूडिनल" निरीक्षण मिळणं हा थोडा नशीबाचाही भाग असेल - पहिल्या वा दुसऱ्या फटक्यातच एखादा मिनिमा सापडणं दर वेळी शक्य नाही. हा मिनिमा फार खोलगट नसेल तर मात्र "क्रॉस सेक्शनल" निरीक्षण दिसेलच असं नाही.
24 Apr 2010 - 7:12 am | धनंजय
काही वैद्यकीय निष्कर्षांसाठी "लाँजिट्यूडिनल" निरीक्षण, जेव्हा असेल तेव्हा ते जास्त प्रबळ असते, हे खरे आहे. अन्य काही विषयांमध्ये सुद्धा असेल. काही विशिष्ट गृहीतके घेतल्यास एककालिक निरीक्षणाचा कालक्रमिक निरीक्षणाशी संबंध लावता येतो.
मात्र एककालिक आणि कालक्रमिक निरीक्षणांची निष्कर्षव्याप्ती एकच नसते. काही कार्यांसाठी एककालिक निरीक्षण लागते तिथे कालक्रमिक निरीक्षण उपयोगाचे नसते. उदाहरणार्थ रोजव्यवहारात - "आता जेवायला वाढायचे का?" असा प्रश्न असताना "आता घरच्या किती लोकांना भूक लागली आहे/जेवायची इच्छा आहे" हे एककालिक निरीक्षण अपेक्षित असते. "बंडूला नेहमीच जास्त भूक लागते", "मंदाला त्या मानाने अग्निमांद्य आहे", वगैरे निरीक्षणे तशी उपयोगी असली तरी दुय्यम आहेत. ("तशी उपयोगी" म्हणजे काय? बंडूला या क्षणी बहुधा भूक लागलेली आहे, आणि मंदाला नाही असा कयास करता येईल. पण ताटे वाढताना प्रत्येकाला "आत्ता भूक लागली आहे का?" हे विचारणे अधिक समर्पक आहे.)
(मात्र बंडू किंवा मंदा यांना औषधोपचार करण्यासाठी "आता भूक लागली आहे का?" असे एककालिक निरीक्षण उपयोगाचे नाही. तिथे कालक्रमिक निरीक्षण आवश्यक आहे.)
वरील प्रयोगात कुठलीही स्पर्धा एककालिकच असते. म्हणजे पहिल्या पिढीतल्या वाक्यांची स्पर्धा नवव्या पिढीतल्या वाक्यांशी नसते. नवव्या पिढीत कुठली वाक्ये असतील त्याबाबत स्पर्धक-खेळाडूंना माहितीसुद्धा नसते. म्हणूनच स्पर्धेचे विश्लेषण एककालिक मोजमापांनी केले तर त्यातून स्पर्धेबद्दल काही विशेष माहिती अपल्याला मिळेल.
मात्र वाक्ये किती पिढ्या दिसतात, त्याच्या कालक्रमिक विश्लेषणाने वाक्यांच्या अंतर्गत टिकाऊपणाबद्दल काही निष्कर्ष काढता येतो.
दोन्ही प्रकारच्या विश्लेषणांमधून वेगळी माहिती मिळते. या प्रयोगामध्ये एककालिकपेक्षा कालक्रमिक बरी, असे नाही. दोन्ही प्रकारची हवी.
25 Apr 2010 - 5:53 am | अक्षय पुर्णपात्रे
कौलस्थिती १ वापरून (१० खेळाडू) एका पिढीतील रंगांच्या शक्यतांचे गणित करून पाहीले. मला खालीलप्रमाणे उत्तरे मिळाली.
जांभळा - २९.९१%
निळा - ४८.७७%
हिरवे - १९.३५%
पिवळे - १.९३%
लाल - ०.०४%
एकूणातच रंगांचे डिस्ट्रिब्युशन काढणे थोडे किचकट आहे.
23 Apr 2010 - 8:39 am | विसोबा खेचर
धन्य आहेस तू धनंजया..
तुझ्या अफाट बुद्धिमत्तेला, व्यासंगाला सलाम..
तात्या.
24 Apr 2010 - 6:09 am | चित्रा
कागदावर गणित (अनॅलिटिकल सोल्यूशन) शक्य आहे, हे माहीत असूनही मी आळस केला. हे गणित मी माँतेकार्लो सिम्युलेशनांनी केले. दहा खेळाडू असलेले १५ पर्यायांचा कौल (अगदी प्रयोगातल्यासारखे) बनवला. प्रत्येक कौलात रँडम यदृच्छेने मते दिली. मते प्रयोगातल्यासारखी मोजली. असे १०,००० कौल खेळले.
छान. :)
प्रयोग आवडला. प्रयोगात भाग घेतल्याने उत्सुकता होती. निष्कर्षही उत्क्रांतीबद्दल अधिक विचार करायला लावणारे आहेत.
25 Apr 2010 - 5:42 am | अक्षय पुर्णपात्रे
प्रत्येक पिढीत खेळाडूंनी दिलेली मते स्मृतीहीन होती. प्रत्येक पिढीतील वाक्यांना (सजीवांना) खेळाडूंनी (परिस्थितीकीने) नव्याने तारले किंवा मारले. हे अपेक्षित असूनही वैशिष्ट्यपूर्ण आहे.