मोजमापं आणि त्रुटी - २

या लेखाचा दुसरा भाग मला चौदा मार्चला, म्हणजे पाय दिनाला प्रसिद्ध करायचा होता. इतर कामांत गुंतलेलो असल्यामुळे थोडा उशीर झाला. आता तुम्ही म्हणाल की या मोजमापांचा आणि 'पाय' चा काय संबंध? उत्तर सोपं आहे. गेल्या लेखात मी तीन आकृती दिल्या होत्या. त्यांच्यातल्या सरळ रेषेची लांबी आणि वक्राकाराची लांबी यांचं गुणोत्तर काढायला सांगितलं होतं. या गुणोत्तरातून पाय ची किंमतच अप्रत्यक्षपणे मोजली जात होती. कशी ते सांगतो.

पाय म्हणजे वर्तुळाचा परीघ भागिले व्यास. व्यास मोजणं सोपं आहे - कारण ती एक सरळ रेषा असते. वर्तुळाचा परीघ मोजणं मात्र सोपं नाही. कारण ती एक वक्र रेषा आहे. त्यामुळे ते मोजण्यासाठी ऍप्रोक्झिमेशन वापरावी लागतात. म्हणजे त्या वर्तुळाचे बारीक बारीक तुकडे करून ते साधारण सरळ रेषा आहेत असं गृहित धरायचं. आणि त्या सर्व तुकड्यांच्या लांबीची बेरीज केली की परीघाचं साधारण उत्तर येतं. जितके बारीक बारीक तुकडे करू तितकं उत्तर अधिकाधिक अचूक येतं. ही पद्धत पूर्वीपासून पायची अधिकाधिक अचूक किंमत काढण्यासाठी वापरलेली आहे. त्या वर्तुळात सामावणारी एक समभुज बहुभुजाकृती काढायची. या बहुभूजाकृतीच्या बाजूंची बेरीज ही जवळपास परीघाइतकी असते असं म्हणता येतं.

आपण सोपं षट्कोनाचं उदाहरण घेऊ. एका वर्तुळाच्या परीघावर समभुज षटकोनाची सहा टोकं ठेवलेली आहेत असं समजू. त्याची प्रत्येक बाजू ही त्या वर्तुळाच्या त्रिज्येइतकी असते. म्हणजे या बहुभुजाकृतीच्या सहा बाजूंची बेरीज ही त्रिज्या * 6 = व्यास * 3 इतकी असते. म्हणजे पायची किंमत येते 3.00. पण षटकोनाच्या बाजूपेक्षा वर्तुळाचा परीघ जास्त आहे हे उघड आहे. म्हणजे पायची किंमत 3 पेक्षा जास्त असली पाहिजे. आता जर आपण त्या वर्तुळाचा कंस हा त्या षटकोनाच्या जीवेच्या किती पट आहे हे मोजलं तर आपल्याला पायची किंमत मोजता येईल. म्हणजे समजा मोजमापं करून जर आपल्याला उत्तर मिळालं की हा कंस त्या जीवेपेक्षा 1.04 पट मोठा आहे, तर पायची किंमत आपल्याला 3.12 इतकी मिळेल. आणि हे गुणोत्तर आपण जितक्या अचूकपणे मोजू तितक्या प्रमाणात पायची किंमत अचूक सापडेल. मी दिलेल्या आकृतीत समभुज दशकोन (आकृती 1), समभुज पंचकोन (आकृती 2), व आणि वीसकोन (आकृती 3) यांची एक भूजा व त्यांबरोबरचे कंस दिले होते. या सर्व आकृतींच्या बाजू त्या वर्तुळाच्या त्रिज्येच्या प्रमाणात मोजता येतात. त्यामुळे षटकोनाच्या उदाहरणाप्रमाणेच जर आपण ते कंस त्या बाजूच्या किती पट आहेत हे मोजलं तर पायची किंमत काढता येते.

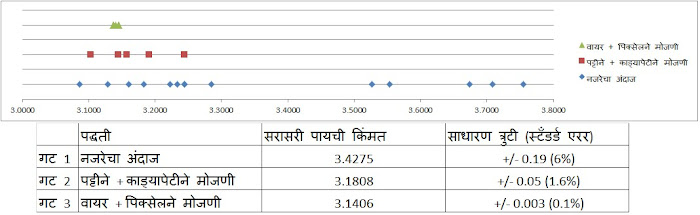या प्रयोगात मला चौघांनी उत्तरं पाठवली. त्यातल्या एका व्यक्तीने फक्त नजरेच्या अंदाजाचं उत्तर पाठवलं. एक उत्तर माझं, अशी पाच वेगवेगळी उत्तरं आहेत. एकंदरीत 27 मोजमापं. चांगलं स्टॅटिस्टिक्स मांडण्यासाठी यापेक्षा अधिक मोजमापं असणं आवश्यक असतं. अर्थात इथे पायची अचूक मोजमापं करणं हा आपला उद्देश नसून मोजमापं आणि त्यांमधल्या त्रुटी याविषयी समजावून घेण्याचा आहे. इतक्या कमी उत्तरांतूनही आपल्याला काही सत्यं गवसतात. प्रथम आपण बाजूचं टेबल व आलेख पाहू. यात मी पाच जणांची मोजमापं तीन वेगळ्या गटांमध्ये टाकलेली आहेत. आलेखात मूळ विदा दाखवलेला आहे. क्ष अक्षावर पायच्या किमती आहेत. तीन रंगांनी प्रत्येक गटातल्या पद्धतींनी मिळालेली उत्तरं दर्शवलेली आहेत. हे गट ठरवताना वापरलेल्या पद्धतीत त्रुटीचं प्रमाण किती आहे यावरून नजरेचा अंदाज सर्वांनीच पाठवला म्हणून ती सर्व मोजमापं एकत्र केलेली आहेत. एका व्यक्तीने मोजमापं करण्यासाठी प्रिंटआउट काढून व पट्टीने कंस मोजला (२-३ सेमी चे छोटे छोटे तुकडे करून व ते सरळ आहेत असे गॄहित धरून.) तर दुसऱ्या व्यक्तीने हीच मोजमापं काड्यापेटीच्या रुंदीने मोजली. या दोन्ही पद्धतींमध्ये मोजमापांतली त्रुटी येते ती पहिलं मोजमाप संपून दुसरं कुठे नक्की सुरू होतं ते बिंदू बरोब्बर जोखण्यात येते. दोन-तीन सेंटीमीटर मोजताना अर्धापाव मिलीमीटरची गल्लत होऊ शकते. त्यामुळे त्यांच्या त्रुटीचं प्रमाण साधारण सारखं आहे - सुमारे एक ते दोन टक्के. म्हणून या पद्धतींचा विचार एकत्र केलेला आहे. एका व्यक्तीने अत्यंत काळजीपूर्वक इअरफोनची वायर शक्य तितक्या अचूकपणे त्या कर्व्हवर ठेवून मोजणी केली. यातल्या त्रुटी म्हणजे वायर कर्व्हच्या किंचित आतबाहेर जाऊ शकते. आणि शेवटचं टोक मोजताना पुन्हा अर्धापाव मिलीमीटरचा फरक येऊ शकतो. अर्थात मोठ्या कागदावर प्रिंटआउट काढला असेल तर ही त्रुटी सुमारे हजारात एकच्या आसपास येते. एका व्यक्तीने हेच मोजमाप ही आकृती जिंपमध्ये उघडून प्रत्येक त्या कर्व्हचे वीसेक भाग करून अंतरं पिक्सेलमध्ये मोजली. याही मोजमापात सुमारे हजारात एकची त्रुटी आहे - कारण या आकृती सुमारे 1600 पिक्सेलच्या आहेत. त्यात एखाददोन पिक्सेलची त्रुटी येऊ शकते. म्हणून या दोन पद्धती एकत्र केल्या.

एक गोष्ट ताबडतोब स्पष्ट होते. डोळ्यांनी केलेल्या अंदाजे मोजमापात प्रचंड व्हेरिएबिलिटी आहे. येणाऱ्या किमती 3.1 ते 3.8 पर्यंत जातात. सोप्या शब्दात सांगायचं झालं तर डोळ्याच्या मोजमापीने उत्तर येतं ते "पायची किंमत सव्वातीन ते पावणेचारच्या दरम्यान कुठेतरी असावी. साधारण साडेतीन." बहुतेक उत्तरं इतर, जास्त अचूक पद्धतीने येणाऱ्या उत्तरांपेक्षा जास्त आहेत. याचा अर्थ डोळ्याने मोजण्याच्या पद्धतीत एक कल (बायस) आहे - वक्राकार अंतरं आहेत त्यापेक्षा थोडी जास्त मोजण्याचा. किंवा सरळ व वक्राकार यांच्यातला फरक आहे त्यापेक्षा जास्त समजण्याचा. दुसऱ्या गटातल्या पद्धती (पट्टी, काड्यापेटी) जास्त नियमित (कन्सिस्टंट) उत्तरं देतात. किंबहुना अत्यंत साध्यासोप्या पद्धतीने मोजमाप करून या पद्धतींनी येणारी उत्तरं ही सरासरी उत्तराच्या सुमारे दीड टक्का कमी-अधिक येतात. म्हणजे "पायची किंमत सुमारे 3.13 ते 3.23 च्या दरम्यान आहे" तिसऱ्या गटातल्या पद्धती (वायर किंवा पिक्सेल) त्याहूनही अधिक नियमित आहेत. या पद्धतींनी येणारी उत्तरं ही सरासरीच्या खूपच जवळ आहेत. त्यांनुसार "पायची किंमत 3.138 ते 3.144' यांच्या दरम्यान आहे. आलेखात असलेले बिंदू अगदी जवळजवळ चिकटलेले दिसतात.

या सगळ्यातून बोध काय मिळतो? पहिल्याप्रथम हे स्पष्ट होतं की आपल्या दृष्टीला काही विशिष्ट मर्यादा आहेत. अंतरं मोजण्याच्या बाबतीत पाच लोकांनी दिलेली उत्तरं ही एकमेकांशी मिळतीजुळती नसतात. त्याहीपलिकडे काही बाबतीत आपला मेंदू ज्या प्रकारे अंतरांचं विश्लेषण करतो त्यात वक्राकार अंतरं जास्त मोजण्याकडे कल आहे. तेव्हा अंतरं अचूक मोजण्यासाठी इतर पद्धती वापरणं अधिक योग्य ठरतं. पण असं असलं तरी आपण डोळ्यांनी मोजलेली अंतरं अगदीच चुकीची नाहीत. सुमारे दहा टक्क्यांची त्रुटी आहे. काही वेळा यापेक्षा अधिक अचूक उत्तराची गरज नसते. वक्राकार रस्त्याने गेलो तर वेळ किती जास्त लागेल याचा प्राथमिक अंदाज पुरेसा असतो. 'एक रस्ता डोंगराला वळसा घालून जाणारा आहे, दुसरा त्या मधून जातो. वळसा घालण्याचं अंतर सुमारे दीडपट आहे, तर चढ-उतारामध्ये सव्वापट जास्त वेळ लागतो' इतपत युक्तिवाद पुरेसा ठरतो. त्यातले दीड किंवा सव्वा हे फार अचूकपणे शोधण्याची गरज नसते. किंवा साधारण वर्तुळाकार भागाला कुंपण घालायचं तर किती सामान लागेल हे उत्तरही फार अचूक असण्याची गरज नाही. दुसऱ्या पद्धतीने अर्थातच 98 ते 99 टक्के 'बरोबर' उत्तर येतं. दैनंदिन जीवनात, किंबहुना इंजिनिअरिंग कॅल्क्युलेशनसाठीही एवढं अचूक उत्तर परेसं आहे. नितीन थत्तेंनी वेळोवेळी हे समजावून सांगितलेलं आहे. तुमच्या अत्यंत अचूक गणितानुसार तुम्हाला आवश्यक असलेल्या रॉडची जाडी जरी 1.1793 सेंटीमीटर आली, तरी बाजारात मिळणारे रॉड हे 1 सेंटीमीटर किंवा 1.25 सेंटीमीटर असतात. अधलंमधलं काही मिळत नाही. तेव्हा जवळातलं जवळ उत्तर हे 1.25 म्हणूनच स्वीकारावं लागतं. यासाठी पायची किंमत 3.1 वापरलीत किंवा 3.14 वापरलीत किंवा 3.18 वापरलीत तरी काहीही फरक पडणार नाही. मात्र तुम्हाला जीपीएस नॅव्हिगेशनसारखी अत्यंत अचूकपणे मोजणारी यंत्रणा बनवायची असेल तर इतकी माया ठेवून चालत नाही. 36000 किमी वरून तुम्हाला अंतरं एक मीटर इतक्या अचूकपणे मोजायची असतील तर पायची किंमत किमान नऊ दशमस्थानांपर्यंत माहित असणं आवश्यक आहे. त्याशिवाय जीपीस यंत्रणा बांधता येणार नाही.

त्रुटी कमी करण्यासाठी जास्त जास्त खर्च करावा लागतो. या तीन आकृतींसाठी डोळ्याने अंदाज अर्ध्या मिनिटात होतो. पट्टीने मोजण्यासाठी पाचेक मिनिटं लागत असावीत. तर पिक्सेलमधलं अंतर काळजीपूर्वक मोजायला अर्धा तास लागतो. जितकी जास्त अचूकता हवी असेल तितक्या प्रमाणात तुमचे कष्ट वाढतात. म्हणजे वाढीव अचूकतेसाठी वाढीव खर्च होतो. तसंच वाढीव अचूकतेसाठी अधिकाधिक आधुनिक उपकरणं लागतात. ही उपकरणं तयार करण्यासाठी आधीच्या उपकरणांनी मोजलेली अचुकता आवश्यक असतात. त्यामुळे मोजमापनातली प्रगती ही आधीच्या मोजमापनांवर आधारित असते. आलेखात मी मांडणी एका उतरंडीप्रमाणे केलेली आहे. ही उतरंड आपल्याला कालानुरुपही अनेक बाबींच्या मोजमापनात दिसते. वरच्या मोजमापांबद्दल बोलताना तुमच्या लक्षात आलं असेल की मी एकदाही 'पायची आदर्श किंमत 3.1415926.... आहे' असं विधान एकाही ठिकाणी केलेलं नाही. या वेगवेगळ्या पद्धतींचा अचुकपणा हा त्या त्या पद्धतीने मिळालेल्या उत्तरांवरून काढला - प्रत्यक्ष पायच्या किमतीशी तुलना करून काढला नाही. याला कारण आहे. पायची किंमत आपल्याला माहित आहे हे खरं आहे. पण इतर अनेक गोष्टी मोजताना आपल्याला आदर्श किंमत माहीत नसते. त्यामुळे मोजमापं ही किती विश्वासार्ह आहेत हे अनेक वेळा मोजमापं करून ठरवावं लागतं. पायचा मुद्दा बाजूला ठेवून एकंदरीत विश्वाच्या ज्ञानाबद्दलही हेच म्हणता येतं. प्राथमिक ज्ञान हे काहीसं डोळ्यांनी केलेल्या मोजमापांप्रमाणे असतं. वेगवेगळ्या लोकांच्या दृष्टिकोनातून जग वेगवेगळं दिसतं. काही समान पैलू असतात, पण व्हेरिएबिलिटी प्रचंड असते. वेगवेगळे कल असल्यामुळे विश्वासार्हताही बरीच कमी असते. त्रुटी भरपूर असते. पण तरीही सर्वसामान्य जीवनात ते उपयुक्त असतं. सूर्य पृथ्वीभोवती फिरतो हे डोळ्यांनी दिसतं. आणि दैनंदिन जीवनात हे ज्ञान उपयुक्त असतं. पण जसजशी जास्त अचूक निरीक्षणं करू तसतसं हे विश्वचित्र चुकीचं आहे, निदान अपुरं आहे असं लक्षात येतं. गॅलिलिओ, कोपर्निकस, न्यूटन वगैरे अनेकांच्या संशोधनांनंतर गुरुत्वाकर्षण, हालचालींचे नियम यांची सांगड घातली जाते आणि न्यूटनचं विश्वचित्र उभं रहातं. पहिल्या चित्रापेक्षा हे कितीतरी अचूक आणि उपयुक्त असतं. आपल्या दुसऱ्या गटातल्या मोजमापांप्रमाणे. पण नंतर आइन्स्टाइन येतो आणि सापेक्षतावादाची मांडणी करून हे चित्र बदलतो. पण बदलतो म्हणजे आधीचं चित्र ठार नष्ट होत नाही. न्यूटन चुकीचा, आइन्स्टाइन बरोबर अशी सरळसोट मांडणी होत नाही. उपयुक्ततेचं क्षेत्र मर्यादित होतं इतकंच. किंवा क्वांटम मेकॅनिक्स आल्यामुळे न्यूटोनियन मेकॅनिक्स चुकीचं ठरत नाही. बिल्डिंग बांधायची, गाडी चालवायची तर न्यूटोनियन मेकॅनिक्सची माहिती पुरेशी ठरते. याउलट सेमिकंडक्टर चिप्स बनवायच्या असतील तर क्वांटम मेकॅनिक्सची गरज पडते. कारण अणुरेणूंच्या पातळीला न्यूटनच्या मेकॅनिक्सची उपयुक्तता संपते. वैज्ञानिक दृष्टिकोनातून ज्ञान म्हणजे काय, थिअरी म्हणजे काय, प्रयोग कसे केले जातात, नवीन थिअरी कशा मांडल्या जातात, जुन्या थिअरींच्या मर्यादा स्पष्ट कशा होतात हे सर्व सांगायला एकदोन लेख पुरणार नाहीत. पण मोजमापं आणि त्रुटी यांच्या अनुषंगाने यातले काही पैलू स्पष्ट झाले असतील अशी आशा आहे.

असो. पाय दिनाच्या सर्वांना (उशीरा का होईना) शुभेच्छा.