आकाश के उस पार भी आकाश है

आपल्याला असा कधी प्रश्न पडला आहे का, की माणूस नेहमी सगळ्या वस्तूंना ठराविक आकारच का देतो? आमची घरे चौकोनी असतात. आमची पुस्तके चौकोनी, संगणकसुद्धा एका विशिष्ट आकाराचा; सगळीकडे चौकोन, आयत, त्रिकोण, गोल हेच आकार. आम्ही एखादे वेळी त्रिकोण किंवा पिरेमिड बांधतो. पण पृथ्वीवर सगळीकडे जमीन उंच-सखल आहे, आम्ही ती सपाट करून टाकतो. खोल भागात भराव टाकतो, डोंगर फोडून काढतो. पण सृष्टी अशी कुठे आहे? कुठला डोंगर अगदी बरोबर त्रिकोणी अथवा शंकू आकाराचा असतो? ढगांना कधी विशिष्ट आकार असतो का? आपले हात, पाय, नाक, डोळे, सगळेच वेगळे आकार. हे आकार आपण भूमितीमध्ये शिकतच नाही. सगळ्या गोष्टींना आपण सोप्या आकृत्यांमध्ये पाहायला शिकतो. लहानपणी आपण माणसाचे चित्र काढताना डोके गोल काढतो. हात-पाय सरळ रेषांनी दाखवतो. किंबहुना भूमितीच्या ठराविक आकृत्यांचा मनावर पगडा बसल्यामुळे आपल्याला सृष्टीमधल्या खऱ्या आकृत्या चित्राच्या रूपात रेखाटणे अवघड जाते.

(आपण काढतो तसे बाळबोध चित्र)

तर ते असो. ह्याबाबत आणखी पुढे सविस्तर बोलूच; पण त्या आधी ऐका एक कहाणी. एक आट-पाट कंपनी होती. तिचे नाव IBM. तिथे मँडेलब्रॉट नावाचा एक हुशार शास्त्रज्ञ काम करीत होता. तसा तो हाडाचा गणितज्ञ, पण भूमितीसह अर्थशास्त्र, माहिती-सिद्धांत (information theory), वहन-यांत्रिकी (fluid mechanics) सारख्या अनेक क्षेत्रांमध्ये त्याने नाक खुपसले होते. तो नेहमी म्हणायचा - "Clouds are not spheres, mountains are not cones, lightening does not travel in a straight line". खरी भूमिती ही उंच-सखलपणा, खड्डे, वळणे, घड्या, गुंता अश्या गोष्टींनी भरलेली आहे. मँडेलब्रॉटचे म्हणणे होते की या सर्व वर-वर अनियमित वाटणाऱ्या गोष्टींना अर्थ आहे आणि यांमध्येच अनेक गोष्टींचे मर्म दडलेले आहे. उदाहरणार्थ समुद्रकिनाऱ्याच्या लांबीचे मर्म काय आहे? मँडेलब्रॉटने असा प्रश्न एका शोधनिबंधामध्ये विचारला कि "ब्रिटनचा समुद्रकिनारा किती लांबीचा आहे?" आणि या प्रश्नाने जणू काही विचारांना नवी दिशाच मिळाली. सांगतो कसे ते.

१९३० च्या दशकात ल्युईस रिचर्डसन या ब्रिटीश शास्त्रज्ञाला समुद्रकिनारे आणि दोन राष्ट्रांमधल्या सीमारेषा यांच्या बद्दल कुतूहल होते. त्याने स्पेन आणि पोर्तुगाल, बेल्जियम आणि नेदरलंडस् या देशांमधले एनसाय्क्लोपिडीया पाहिले आणि त्याच्या असे ध्यानात आले की सामायिक (common) सीमारेषा असल्या तरी दोन देशांच्या नोंदींमध्ये (सीमारेषांची लांबी) साधारण २० टक्क्यांचा फरक आहे. अनेकांना तो खोटा वाटला. काहीजण म्हणाले, 'असेल बुवा. हे काही माझे क्षेत्र नाही'; काहीजण म्हणाले, 'मी एनसाय्क्लोपिडीया बघून सांगतो.' मँडेलब्रॉटच्या वाचनात हा लेख आला. त्याचे काय म्हणणे होते, की कुठलीही भौगोलिक सीमा ही एका अर्थाने अनंत लांबीची असते. दुसऱ्या शब्दात सांगायचे तर तुम्ही मोजमापासाठी कोणती पट्टी वापरता त्यावर तुम्ही मोजलेली एकूण लांबी किती भरेल हे ठरते.

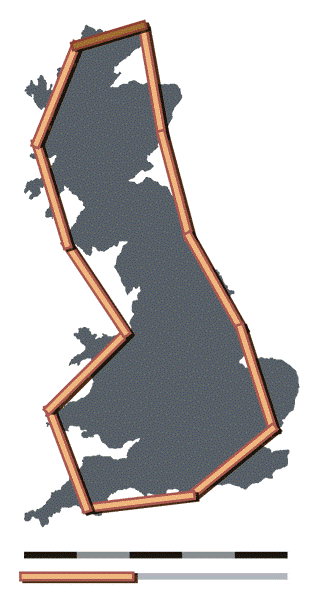
(अ)

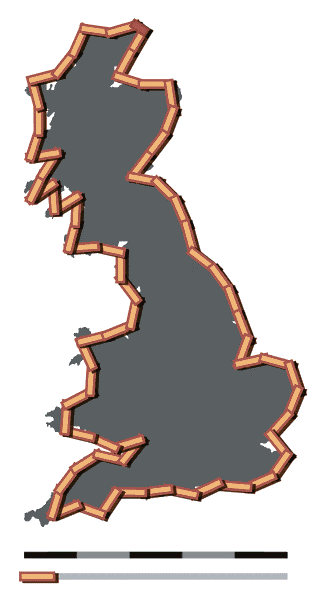
(आ)
(ब्रिटनच्या समुद्रकिनाऱ्याची लांबी मोजायचा एक प्रयत्न (अ) एक २०० किलोमीटर लांबीची पट्टी वापरून आणि (आ) एक ५० किलोमीटर लांबीची पट्टी वापरून)

आता एक प्रात्यक्षिकच पाहू. वर दिलेल्या आकृती (अ) मध्ये ती लांबी मोजण्यासाठी २०० कि.मी. लांबीची पट्टी वापरली आहे, तर (आ) मध्ये ५० कि.मी. लांबीची पट्टी. (अ) मधल्या पट्टीने मोजल्यास एकूण लांबी २४०० किलोमीटर भरते तर (आ) मधल्या पट्टीने मोजल्यास ती ३४०० किलोमीटर भरते. इथे आपल्या डोळ्यांना सहज लक्षात येण्यासारखी गोष्ट आहे कि २०० कि.मी. ची पट्टी बरीच वळणे, ओबड-धोबडपणा पाहू शकत नाही. आता आपण पट्टी आणखी छोटी करत गेलो, तर आणखीन छोटी छोटी नागमोडी वळणे आपण मोजू शकू. पट्टी जितकी छोटी तितके जास्त बारकावे आपल्याला कळतील आणि एकूण लांबीचा आकडा तितकाच जास्त फुगत जाईल. दूर यानातून आपल्याला जितकी लांबी मोजता येईल, त्यापेक्षा जास्त लांबी समुद्र-किनाऱ्यावर चालत फिरणारा माणूस मोजू शकेल. त्याही पेक्षा जास्त लांबी एकेक खडा पार करत जाणारी गोगलगाय मोजू शकेल (अर्थात तिला तितका संयम हवा).

आता काही वेळापुरते आपण भूमितीकडे वळू आणि नंतर पुन्हा या भौगोलिक प्रश्नाकडे येऊ. त्याचे काय झाले, की १९व्या शतकाच्या सुरुवातीला 'कोख' नावाचा एक स्वीडिश गणितज्ञ होऊन गेला. त्याने आकृत्यांबाबत अनेक खेळ केले. त्याच्या नावाने 'कोखचा वक्र’ (Koch's curve) म्हणून एक आकृती ओळखली जाते. अत्यंत सोपी, पण त्यात एक मर्म दडले आहे अशी ही आकृती. ती कशी आहे ते आता आपण पाहू.

सुरुवातीला एक त्रिकोण घ्या. (त्याच्या प्रत्येक बाजूची लांबी '३' इतकी आहे असे आपण समजू. त्या ३ ला परिमाण काय हवे ते! म्हणजे त्रिकोणाची परिमिती ९ इतकी झाली.) त्याची प्रत्येक बाजू तिनात भागा. आता प्रत्येक मधल्या छोट्या भागावर आणखी एक छोटा त्रिकोण बांधा (ज्याची प्रत्येक बाजू अर्थात १ इतकी असेल). तयार झालेल्या आकृतीची बाह्य परिमिती १२ इतकी होईल. अशातऱ्हेने त्या छोट्या त्रिकोणांनाही भागून त्यांच्यावर आणखी छोटे छोटे त्रिकोण बांधत राहिल्यास पुढची बाह्य परिमिती १६ इतकी होईल. (बाह्य परिमिती म्हणजे काय? - खाली दिलेल्या आकृत्यांमध्ये केवळ काळ्या रंगाच्या रेषा पहा).

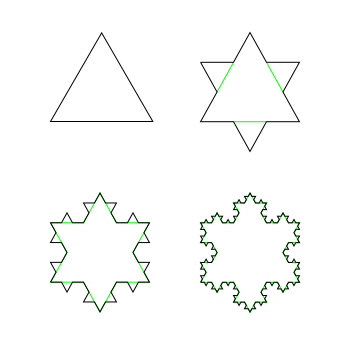
(त्रिकोणापासून सुरुवात करून त्यावर आणखीन छोटे छोटे असे त्रिकोण रचत गेल्यास मिळणारी आकृती)

म्हणजे थोडक्यात, आपण जसे आणखी छोटे छोटे त्रिकोण बांधत जाऊ, तशी नवीन आकृतीची परिमिती आधीच्या आकृतीच्या ४/३ पट होते. आता असे छोटे छोटे त्रिकोण अनंत काळ बांधत बसल्यास एकूण परिमिती ४/३ च्या पटीत वाढत वाढत जाऊन अनंत होईल. याच आकृतीचे नाव ‘कोखचा वक्र’. गंमत म्हणजे पहिल्या त्रिकोणाच्या तीनही बिंदूंमधून जाणारे एक वर्तुळ काढले तर असे लक्षात येईल की आपण पुढे कितीही त्रिकोण-त्रिकोण वाढवत बसलो तरी संपूर्ण आकृती त्या वर्तुळाच्या आतच राहते आहे. म्हणजे ही अनंत लांबीची रेषा एका छोट्याच्या वर्तुळाच्या आताच वस्ती करून बसली आहे!

आता आपण एक काम करू. ह्या आकृतीच्या कोणत्याही एका भागात भिंगाने पाहण्याचा प्रयत्न करू. खाली दिलेल्या आकृतीमध्ये एकेका चित्रात त्यातील छोटे भाग हळू-हळू मोठे करून दाखवले आहेत. ते पाहता असे लक्षात येईल की जसे जसे आपण त्या आकृतीच्या आत जात राहू तसे तसे तोच तोच आकार आपल्याला दिसतो आहे. ह्या प्रकाराला 'स्व-साधर्म्य' (self-similarity) असे म्हटले जाते. म्हणजे एखादी आकृती लांबून जशी दिसते, तशीच ती जवळूनही दिसते. तिला कितीही सूक्ष्मतर रुपात पाहत जाऊ, ती तशीच दिसते.

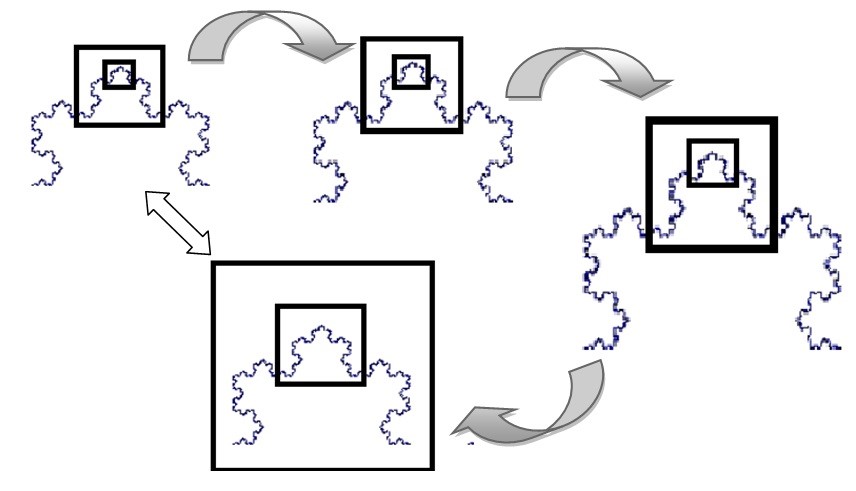
अश्या आकृत्यांमध्ये नागमोडी वळणे आपल्याला लांबून दिसत नाहीत, पण जवळ जाता ते दृष्टिगोचर होतात. जितके त्याच्या आत शिरू तितकी आणखी नागमोडी वळणे दिसायला लागतात. हेच ते कारण ज्यामुळे मँडेलब्रॉट म्हणाला कि समुद्रकिनाऱ्याची लांबी अनंत आहे. (वास्तविक ह्या आत आत शिरण्याला मर्यादा आहेत. कोणती तरी अशी स्थिती येईल ज्यापुढे ह्या रेषेची एकसंधता तुटेल.).

पण यावरून मँडेलब्रॉटच्या असे लक्षात आले की हे स्वसाधर्म्य अनेक गोष्टी विषद करू शकेल. ह्या स्वसाधर्म्याचा गुणधर्म वस्तूंना एका ठराविक छोट्या आकारात सामावून देखील खूप मोठी लांबी देतो. मग याची पुढची पायरी येते ती म्हणजे त्रिमितीमध्ये (3D) ठराविक आकाराच्या आत प्रचंड मोठे क्षेत्र सामावून दाखवणे. एक गंमत म्हणून तुम्ही स्वतः अशी एखादी आकृती काढून पहायचा प्रयत्न करू शकता. किंवा पुढच्या भागाची प्रतीक्षा करा.

या स्वसाधर्म्यामुळे मँडेलब्रॉट जणू काही सगळीकडे तेच पाहू लागला. जळी-स्थळी-काष्ठी-पाषाणी सगळीकडे स्वसाधर्म्य! झाडाच्या पानांत, फुलाच्या पाकळ्यांत इतकेच नाही तर आपल्या शरीरात - रक्तवाहिनींच्या जाळ्यात, फुफ्फुसांच्या जंजाळात - सगळीकडे एक नवीन प्रकारची भूमिती वसते आहे. युक्लीडच्या १, २ किंवा ३ मिती त्या भूमितीला विषद करण्यास अपुऱ्या आहेत. ह्यातूनच 'अपूर्णांक भूमिती (Fractals)' ह्या नवीन भूमितीचा जन्म झाला. ह्या भूमितीने जगाकडे पाहण्याचा एक वेगळाच दृष्टीकोन दिला. लताचे 'आकाश के उस पार भी आकाश है' हे गाणे ऐकताना त्यामागे स्वसाधर्म्य किंवा अपूर्णांक भूमितीच आहे की काय असा मला भास झाला. काय आहे ही भूमिती? पाना-फुलात, रक्तवाहिन्यात तिचा काय उपयोग ? पाहूया पुढच्या भागात.

- शंतनु
(काही वर्षांपूर्वी मी इथेच 'हलकल्लोळ' या नावाने हाच लेख अर्धवट लिहिला होता. तो डागडुजी करून पूर्ण केला आहे. आता पुढचा लेख टाकायला तेवढा वेळ लावणार नाही.)
मूळ लेख माझ्या स्वतःच्या ब्लॉगवरून पुनःप्रकाशित. हा लेख इतरत्रही प्रकाशित.
Material licensed under a Creative Commons Attribution-NoDerivatives 4.0 International.
(तिसरे रेखाचित्र सोडून सर्व चित्रे विकिपिडीयावरून साभार)

क्रमशः